Markowitz Portfolio Optimization¶

When it comes to investing, one of the most fundamental questions is: How can I build a portfolio that gives me the best return with the least amount of risk? The answer to this question lies in the work of Harry Markowitz, a financial economist whose theories revolutionized the way we approach portfolio management. Markowitz's Portfolio Theory, often referred to as the Markowitz Efficient Frontier, provides a framework for finding that balance using a mathematical approach to optimizing investments.

What Is Markowitz Portfolio Optimization?¶

At its core, Markowitz Portfolio Optimization is about finding the right mix of assets that will give you the highest expected return for a given level of risk (or the least risk for a given return). The theory suggests that investors should not look at individual investments in isolation, but rather, how they work together in a portfolio.

Markowitz’s main contribution was the realization that combining different types of investments — stocks, bonds, real estate, etc. — can reduce the overall risk of a portfolio without necessarily lowering its expected return. This insight came from understanding that assets do not move in perfect harmony. Some investments rise when others fall, and this diversification can smooth out the bumps of the market, creating a more stable, efficient investment strategy.

Key Concepts¶

Risk and Return¶

Risk and return are two sides of the same coin. In simple terms:

• Return is the gain or profit you expect from your investments.
• Risk is the uncertainty or potential for loss in an investment. This is often measured by volatility, or how much an investment’s value fluctuates.

The fundamental goal of Markowitz’s theory is to find the optimal combination of assets that maximizes return for a given level of risk.

Diversification¶

Diversification is the cornerstone of Markowitz’s theory. By holding a variety of investments, you reduce the impact of any single asset’s performance on the overall portfolio. The key is to choose assets that don’t move in the same direction. For example, when stock prices are falling, bond prices may be rising. By combining assets with low or negative correlations, you can lower the portfolio's risk.

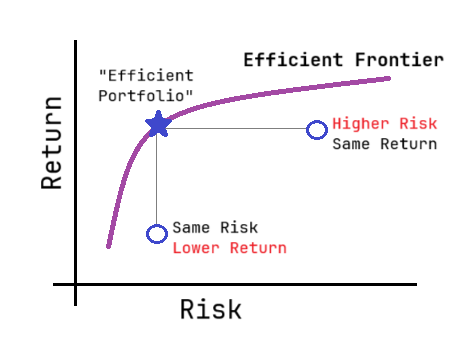
The Efficient Frontier¶

The Efficient Frontier is a curve that shows the optimal portfolios offering the highest expected return for a given level of risk. Portfolios below this curve are suboptimal, as they either offer lower returns for the same risk or higher risk for the same return.

• Graph Axes:

  • The x-axis is Risk
  • The y-axis is Return

• The Curve

  • The curve starts at the least risky portfolio and curves upward as you take on more risk for higher returns.
  • Portfolios below the curve are bad deals—they have too much risk for the return they offer.
  • Portfolios on the curve are the best deals—they balance risk and return.

Benefits and Limitations¶

Benefits¶

• Encourages diversification, reducing portfolio risk.
• Provides a systematic, data-driven approach to portfolio construction.
• Helps visualize trade-offs between risk and return.

Limitations¶

• Assumes historical data predicts future performance.
• Relies on estimates of returns and covariances, which can be inaccurate.
• Treats risk as variance, which penalizes upside volatility (positive surprises).

The Markowitz Optimization Model¶

Portfolio Return¶

The expected return of a portfolio is the weighted sum of the individual asset returns:
$$ E(R_p) = \sum_{i=1}^n w_i E(R_i) $$
Here:

• $ E(R_p) $: Portfolio’s expected return
• $ w_i $: Weight (percentage) of the portfolio invested in asset $i$
• $ E(R_i) $: Expected return of asset $i$

Portfolio Risk (Variance)¶

Risk is captured by the variance (or standard deviation) of returns. For a portfolio:
$$ \sigma_p^2 = \sum_{i=1}^n \sum_{j=1}^n w_i w_j \text{Cov}(R_i, R_j) $$
Where:

• $ \sigma_p^2 $: Portfolio variance
• $ \text{Cov}(R_i, R_j) $: Covariance between the returns of assets $i$ and $j$
  Covariance measures how the returns of two assets move together. Diversification benefits arise when assets are negatively correlated or have low covariance.

The Optimization Problem¶

The goal is to solve this constrained optimization problem:

$$ \text{Maximize } E(R_p) \text{ for a given level of } \sigma_p^2 $$

Or equivalently:

$$ \text{Minimize } \sigma_p^2 \text{ for a given level of } E(R_p) $$

Subject to:

1. $\sum_{i=1}^n w_i = 1$ (The weights must sum to 1, i.e., you invest all your money.)
2. $w_i \geq 0$ (Non-negativity constraint if short-selling is not allowed.)

Python model¶

Import libraries¶

In [1]:

# Import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yfin
from scipy.optimize import minimize
import warnings
warnings.filterwarnings('ignore')

# Import libraries import numpy as np import pandas as pd import matplotlib.pyplot as plt import yfinance as yfin from scipy.optimize import minimize import warnings warnings.filterwarnings('ignore')

Download data¶

We are going to use 10 different stocks in several sectors (Technology, Healthcare, Finance, and Retail)

In [2]:

stocks = [
    {"symbol": "AAPL", "name": "Apple Inc."},
    {"symbol": "MSFT", "name": "Microsoft Corporation"},
    {"symbol": "AMZN", "name": "Amazon.com Inc."},
    {"symbol": "TSLA", "name": "Tesla Inc."},
    {"symbol": "JNJ", "name": "Johnson & Johnson"},
    {"symbol": "PFE", "name": "Pfizer Inc."},
    {"symbol": "JPM", "name": "JPMorgan Chase & Co."},
    {"symbol": "V", "name": "Visa Inc."},
    {"symbol": "PG", "name": "Procter & Gamble Co."},
    {"symbol": "XOM", "name": "Exxon Mobil Corporation"}
]

stocks = [ {"symbol": "AAPL", "name": "Apple Inc."}, {"symbol": "MSFT", "name": "Microsoft Corporation"}, {"symbol": "AMZN", "name": "Amazon.com Inc."}, {"symbol": "TSLA", "name": "Tesla Inc."}, {"symbol": "JNJ", "name": "Johnson & Johnson"}, {"symbol": "PFE", "name": "Pfizer Inc."}, {"symbol": "JPM", "name": "JPMorgan Chase & Co."}, {"symbol": "V", "name": "Visa Inc."}, {"symbol": "PG", "name": "Procter & Gamble Co."}, {"symbol": "XOM", "name": "Exxon Mobil Corporation"} ]

In [3]:

symbols = [st['symbol'] for st in stocks]

symbols = [st['symbol'] for st in stocks]

In [4]:

# Download the Daily closing price for the last 10 years
stock_df = yfin.download(symbols, period="10y")['Adj Close']

# Download the Daily closing price for the last 10 years stock_df = yfin.download(symbols, period="10y")['Adj Close']

[*********************100%%**********************]  10 of 10 completed

In [5]:

stock_df

stock_df

Out[5]:

Ticker	AAPL	AMZN	JNJ	JPM	MSFT	PFE	PG	TSLA	V	XOM
Date
2014-11-24	26.418226	16.782000	81.752777	46.244347	40.865200	19.331116	66.516785	16.448000	59.352398	61.911777
2014-11-25	26.188854	16.752001	81.615082	45.743679	40.762161	19.491039	67.037674	16.539333	59.967785	61.303799
2014-11-26	26.500629	16.678499	82.005203	45.774017	41.002590	19.894043	67.098068	16.562668	59.967785	61.109768
2014-11-28	26.485031	16.931999	82.800697	45.637470	41.054115	19.926027	68.268211	16.301332	60.184582	58.561356
2014-12-01	25.625439	16.299999	82.632408	45.516094	41.749657	19.996380	68.003967	15.442667	60.175240	59.732059
...	...	...	...	...	...	...	...	...	...	...
2024-11-18	228.020004	201.699997	154.770004	245.029999	414.929474	24.860001	170.750000	338.739990	312.160004	120.309998
2024-11-19	228.279999	204.610001	153.000000	243.089996	416.955414	25.100000	170.759995	346.000000	311.850006	118.629997
2024-11-20	229.000000	202.880005	153.110001	240.779999	414.659973	24.940001	170.889999	342.029999	307.390015	120.320000
2024-11-21	228.520004	198.380005	155.500000	244.759995	412.869995	25.129999	172.750000	339.640015	309.899994	121.930000
2024-11-22	230.514999	198.095001	155.020004	248.419998	415.035004	25.605000	177.399994	354.250000	308.684998	121.940002

2517 rows × 10 columns

In [6]:

stock_df.info()

stock_df.info()

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 2517 entries, 2014-11-24 to 2024-11-22
Data columns (total 10 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   AAPL    2517 non-null   float64
 1   AMZN    2517 non-null   float64
 2   JNJ     2517 non-null   float64
 3   JPM     2517 non-null   float64
 4   MSFT    2517 non-null   float64
 5   PFE     2517 non-null   float64
 6   PG      2517 non-null   float64
 7   TSLA    2517 non-null   float64
 8   V       2517 non-null   float64
 9   XOM     2517 non-null   float64
dtypes: float64(10)
memory usage: 216.3 KB

In [7]:

# plot stock closing price over time
stock_df.plot(figsize=(10,5));

# plot stock closing price over time stock_df.plot(figsize=(10,5));

Daily Returns¶

Now, we are going to calculate the daily returns of these stocks

In [8]:

daily_returns = stock_df.pct_change(1).dropna()
daily_returns.plot(figsize=(10,5));

daily_returns = stock_df.pct_change(1).dropna() daily_returns.plot(figsize=(10,5));

In [9]:

daily_returns['AAPL'].plot(kind='hist',bins=100,figsize=(12,3));

daily_returns['AAPL'].plot(kind='hist',bins=100,figsize=(12,3));

Cumulative Returns¶

In [10]:

cumulative_returns = (1 + daily_returns).cumprod() - 1
cumulative_returns_perc = cumulative_returns*100
cumulative_returns_perc.plot(figsize=(10,5));

cumulative_returns = (1 + daily_returns).cumprod() - 1 cumulative_returns_perc = cumulative_returns*100 cumulative_returns_perc.plot(figsize=(10,5));

Log Returns¶

In [11]:

# Log Returns as Percent of next day
log_returns = np.log(stock_df/stock_df.shift(1))
log_returns

# Log Returns as Percent of next day log_returns = np.log(stock_df/stock_df.shift(1)) log_returns

Out[11]:

Ticker	AAPL	AMZN	JNJ	JPM	MSFT	PFE	PG	TSLA	V	XOM
Date
2014-11-24	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2014-11-25	-0.008720	-0.001789	-0.001686	-0.010886	-0.002525	0.008239	0.007800	0.005537	0.010315	-0.009869
2014-11-26	0.011835	-0.004397	0.004769	0.000663	0.005881	0.020466	0.000900	0.001410	0.000000	-0.003170
2014-11-28	-0.000589	0.015085	0.009654	-0.002988	0.001256	0.001606	0.017289	-0.015904	0.003609	-0.042597
2014-12-01	-0.032994	-0.038040	-0.002035	-0.002663	0.016800	0.003524	-0.003878	-0.054113	-0.000155	0.019794
...	...	...	...	...	...	...	...	...	...	...
2024-11-18	0.013333	-0.004502	0.004988	-0.001142	0.001830	0.002416	0.007112	0.054664	0.008106	0.008347
2024-11-19	0.001140	0.014324	-0.011502	-0.007949	0.004871	0.009608	0.000059	0.021206	-0.000994	-0.014062
2024-11-20	0.003149	-0.008491	0.000719	-0.009548	-0.005520	-0.006395	0.000761	-0.011540	-0.014405	0.014145
2024-11-21	-0.002098	-0.022430	0.015489	0.016394	-0.004326	0.007589	0.010825	-0.007012	0.008132	0.013292
2024-11-22	0.008692	-0.001438	-0.003092	0.014843	0.005230	0.018725	0.026562	0.042117	-0.003928	0.000082

2517 rows × 10 columns

In [12]:

# Notice how close this is to our original returns!
stock_df.pct_change(1)

# Notice how close this is to our original returns! stock_df.pct_change(1)

Out[12]:

Ticker	AAPL	AMZN	JNJ	JPM	MSFT	PFE	PG	TSLA	V	XOM
Date
2014-11-24	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2014-11-25	-0.008682	-0.001788	-0.001684	-0.010827	-0.002521	0.008273	0.007831	0.005553	0.010368	-0.009820
2014-11-26	0.011905	-0.004388	0.004780	0.000663	0.005898	0.020676	0.000901	0.001411	0.000000	-0.003165
2014-11-28	-0.000589	0.015199	0.009701	-0.002983	0.001257	0.001608	0.017439	-0.015779	0.003615	-0.041702
2014-12-01	-0.032456	-0.037326	-0.002032	-0.002660	0.016942	0.003531	-0.003871	-0.052675	-0.000155	0.019991
...	...	...	...	...	...	...	...	...	...	...
2024-11-18	0.013422	-0.004491	0.005000	-0.001141	0.001831	0.002419	0.007137	0.056186	0.008138	0.008382
2024-11-19	0.001140	0.014427	-0.011436	-0.007917	0.004883	0.009654	0.000059	0.021432	-0.000993	-0.013964
2024-11-20	0.003154	-0.008455	0.000719	-0.009503	-0.005505	-0.006374	0.000761	-0.011474	-0.014302	0.014246
2024-11-21	-0.002096	-0.022181	0.015610	0.016530	-0.004317	0.007618	0.010884	-0.006988	0.008165	0.013381
2024-11-22	0.008730	-0.001437	-0.003087	0.014953	0.005244	0.018902	0.026917	0.043016	-0.003921	0.000082

2517 rows × 10 columns

MonteCarlo simulation for Optimization Search¶

Generating Random Weights¶

In [13]:

def gen_weights(n):
    source = np.random.random(n)
    # pos = np.random.randint(0,n)
    # source[pos] = 10
    weights = np.random.dirichlet(source,size=1)
    return np.array(weights[0])

def gen_weights(n): source = np.random.random(n) # pos = np.random.randint(0,n) # source[pos] = 10 weights = np.random.dirichlet(source,size=1) return np.array(weights[0])

Portfolio Returns Function¶

In [14]:

def calculate_returns(weights):
    return np.sum(log_returns.mean()*weights) * 252 #Annualized Returns

def calculate_returns(weights): return np.sum(log_returns.mean()*weights) * 252 #Annualized Returns

Portfolio Volatility (Variance) Function¶

In [15]:

log_returns_cov = log_returns.cov()  # Covariance
def calculate_volatility(weights):
    annualized_cov = np.dot(log_returns_cov*252,weights)
    vol = np.dot(weights.transpose(),annualized_cov)
    return np.sqrt(vol)

log_returns_cov = log_returns.cov() # Covariance def calculate_volatility(weights): annualized_cov = np.dot(log_returns_cov*252,weights) vol = np.dot(weights.transpose(),annualized_cov) return np.sqrt(vol)

Montecarlo¶

Now we just create many, many random weightings, and we can then plot them on expected return vs. expected volatility (coloring them by Sharpe Ratio):

In [16]:

n = len(stock_df.columns)
mc_portfolio_returns = []
mc_portfolio_vol = []
mc_weights = []
for sim in range(100000):
    # This may take a while!
    weights = gen_weights(n)
    mc_weights.append(weights)
    mc_portfolio_returns.append(calculate_returns(weights))
    mc_portfolio_vol.append(calculate_volatility(weights))

n = len(stock_df.columns) mc_portfolio_returns = [] mc_portfolio_vol = [] mc_weights = [] for sim in range(100000): # This may take a while! weights = gen_weights(n) mc_weights.append(weights) mc_portfolio_returns.append(calculate_returns(weights)) mc_portfolio_vol.append(calculate_volatility(weights))

In [17]:

# Sharpe Ratios
mc_sharpe_ratios = np.array(mc_portfolio_returns)/np.array(mc_portfolio_vol)

# Sharpe Ratios mc_sharpe_ratios = np.array(mc_portfolio_returns)/np.array(mc_portfolio_vol)

In [18]:

# Plot Results
plt.figure(dpi=200,figsize=(10,5))
plt.scatter(mc_portfolio_vol,mc_portfolio_returns,c=mc_sharpe_ratios)
plt.ylabel('Expected Returns')
plt.xlabel('Expected Volatility')
plt.colorbar(label='Sharpe Ratio');

# Plot Results plt.figure(dpi=200,figsize=(10,5)) plt.scatter(mc_portfolio_vol,mc_portfolio_returns,c=mc_sharpe_ratios) plt.ylabel('Expected Returns') plt.xlabel('Expected Volatility') plt.colorbar(label='Sharpe Ratio');

In [19]:

# Portfolio from the MonteCarlo simulation that maximizes the Sharpe Ratio 
portfolio_mc_sr = mc_weights[np.argmax(mc_sharpe_ratios)]
portfolio_mc_sr

# Portfolio from the MonteCarlo simulation that maximizes the Sharpe Ratio portfolio_mc_sr = mc_weights[np.argmax(mc_sharpe_ratios)] portfolio_mc_sr

Out[19]:

array([4.72203516e-02, 1.36616169e-01, 2.09472211e-02, 1.87584923e-01,
       3.99647867e-01, 4.05349264e-09, 1.38906542e-01, 6.74778789e-02,
       1.59904258e-03, 4.00561676e-12])

Optimal Weighting through Minimization Search¶

In [20]:

# Objective Function
def objective(weight):
    # Note -1* because we are minimizing. It is the same as maximizing the positive sharpe ratio
    return -1 * (calculate_returns(weight)/calculate_volatility(weight))

# Objective Function def objective(weight): # Note -1* because we are minimizing. It is the same as maximizing the positive sharpe ratio return -1 * (calculate_returns(weight)/calculate_volatility(weight))

In [21]:

# Bounds of the decision variables (weights)
bounds = tuple((0,1) for _ in range(n))

# Bounds of the decision variables (weights) bounds = tuple((0,1) for _ in range(n))

In [22]:

# Constraint - All weights to add up to 1
sum_constraint = ({'type': 'eq', 'fun': lambda weight: np.sum(weight)-1})

# Constraint - All weights to add up to 1 sum_constraint = ({'type': 'eq', 'fun': lambda weight: np.sum(weight)-1})

In [23]:

# Starting Guess
equal_weights = n * [1/n]

# Starting Guess equal_weights = n * [1/n]

In [24]:

results = minimize(fun=objective,x0=equal_weights,bounds=bounds,constraints=sum_constraint)

results = minimize(fun=objective,x0=equal_weights,bounds=bounds,constraints=sum_constraint)

In [25]:

portfolio_optimal_sr = results.x
portfolio_optimal_sr

portfolio_optimal_sr = results.x portfolio_optimal_sr

Out[25]:

array([1.13971593e-01, 1.94361952e-01, 0.00000000e+00, 1.71332999e-01,
       2.55048319e-01, 9.63313630e-17, 2.09921478e-01, 5.53636596e-02,
       2.03287907e-18, 6.27482007e-18])

Results comparison¶

In [26]:

# Create x-axis positions for groups
x = np.arange(n)  # Positions for each stock
width = 0.4  # Width of each bar

# Create the bar plot
plt.figure(figsize=(10, 5))
plt.bar(x - width/2, portfolio_mc_sr, width, label='MonteCarlo')  # Portfolio from MonteCarlo simulation
plt.bar(x + width/2, portfolio_optimal_sr, width, label='Minimization')   # Portfolio from minimization solution

# Add labels, title, and legend
plt.xlabel('Stock', fontsize=12)
plt.ylabel('Weight', fontsize=12)
plt.title('Optimal Portfolio based on Sharpe Ratio', fontsize=14)
plt.xticks(x, symbols, fontsize=10)  # Set x-ticks to the names
plt.legend(fontsize=10)

# Show the plot
plt.tight_layout()  # Adjust layout to prevent label overlap
plt.show()

# Create x-axis positions for groups x = np.arange(n) # Positions for each stock width = 0.4 # Width of each bar # Create the bar plot plt.figure(figsize=(10, 5)) plt.bar(x - width/2, portfolio_mc_sr, width, label='MonteCarlo') # Portfolio from MonteCarlo simulation plt.bar(x + width/2, portfolio_optimal_sr, width, label='Minimization') # Portfolio from minimization solution # Add labels, title, and legend plt.xlabel('Stock', fontsize=12) plt.ylabel('Weight', fontsize=12) plt.title('Optimal Portfolio based on Sharpe Ratio', fontsize=14) plt.xticks(x, symbols, fontsize=10) # Set x-ticks to the names plt.legend(fontsize=10) # Show the plot plt.tight_layout() # Adjust layout to prevent label overlap plt.show()

In [27]:

# Historical performance
mc_sr_returns = np.dot(portfolio_mc_sr,daily_returns.transpose())
optimal_sr_returns = np.dot(portfolio_optimal_sr,daily_returns.transpose())
# Cumulative returns
cumulative_mc_sr_returns = (1 + mc_sr_returns).cumprod() - 1
cumulative_mc_sr_returns_perc = pd.Series(cumulative_mc_sr_returns*100, index=daily_returns.index)
cumulative_optimal_sr_returns = (1 + optimal_sr_returns).cumprod() - 1
cumulative_optimal_sr_returns_perc = pd.Series(cumulative_optimal_sr_returns*100, index=daily_returns.index)

cumulative_mc_sr_returns_perc.plot(figsize=(10,5), label='MonteCarlo')
cumulative_optimal_sr_returns_perc.plot(figsize=(10,5), label='Optimization')
plt.title('Historical Performance', fontsize=14)
plt.legend(fontsize=10);

# Historical performance mc_sr_returns = np.dot(portfolio_mc_sr,daily_returns.transpose()) optimal_sr_returns = np.dot(portfolio_optimal_sr,daily_returns.transpose()) # Cumulative returns cumulative_mc_sr_returns = (1 + mc_sr_returns).cumprod() - 1 cumulative_mc_sr_returns_perc = pd.Series(cumulative_mc_sr_returns*100, index=daily_returns.index) cumulative_optimal_sr_returns = (1 + optimal_sr_returns).cumprod() - 1 cumulative_optimal_sr_returns_perc = pd.Series(cumulative_optimal_sr_returns*100, index=daily_returns.index) cumulative_mc_sr_returns_perc.plot(figsize=(10,5), label='MonteCarlo') cumulative_optimal_sr_returns_perc.plot(figsize=(10,5), label='Optimization') plt.title('Historical Performance', fontsize=14) plt.legend(fontsize=10);

In [28]:

# Plot the histogram
plt.figure(figsize=(12, 3))
plt.hist(mc_sr_returns, bins=100, label='MonteCarlo')
plt.hist(optimal_sr_returns, bins=100, alpha=0.7, label='Minimization')
plt.legend(fontsize=10)
# Show the plot
plt.tight_layout()
plt.show()

# Plot the histogram plt.figure(figsize=(12, 3)) plt.hist(mc_sr_returns, bins=100, label='MonteCarlo') plt.hist(optimal_sr_returns, bins=100, alpha=0.7, label='Minimization') plt.legend(fontsize=10) # Show the plot plt.tight_layout() plt.show()

In [29]:

stats = {
    'Montecarlo': {
        'Returns': calculate_returns(portfolio_mc_sr),
        'Volatility': calculate_volatility(portfolio_mc_sr),
        'Sharpe Ratio': calculate_returns(portfolio_mc_sr)/calculate_volatility(portfolio_mc_sr)
    },
    'Minimization': {
        'Returns': calculate_returns(portfolio_optimal_sr),
        'Volatility': calculate_volatility(portfolio_optimal_sr),
        'Sharpe Ratio': calculate_returns(portfolio_optimal_sr)/calculate_volatility(portfolio_optimal_sr)
    }
}
pd.DataFrame(stats)

stats = { 'Montecarlo': { 'Returns': calculate_returns(portfolio_mc_sr), 'Volatility': calculate_volatility(portfolio_mc_sr), 'Sharpe Ratio': calculate_returns(portfolio_mc_sr)/calculate_volatility(portfolio_mc_sr) }, 'Minimization': { 'Returns': calculate_returns(portfolio_optimal_sr), 'Volatility': calculate_volatility(portfolio_optimal_sr), 'Sharpe Ratio': calculate_returns(portfolio_optimal_sr)/calculate_volatility(portfolio_optimal_sr) } } pd.DataFrame(stats)

Out[29]:

	Montecarlo	Minimization
Returns	0.204399	0.198496
Volatility	0.214235	0.206010
Sharpe Ratio	0.954086	0.963527

Efficient Frontier¶

The efficient frontier is the set of optimal portfolios that offers the highest expected return for a defined level of risk or the lowest risk for a given level of expected return. Portfolios that lie below the efficient frontier are sub-optimal, because they do not provide enough return for the level of risk. Portfolios that cluster to the right of the efficient frontier are also sub-optimal, because they have a higher level of risk for the defined rate of return

In [30]:

# Expected Return Range
expected_returns_range = np.linspace(0.01,0.35,100)

# Expected Return Range expected_returns_range = np.linspace(0.01,0.35,100)

In [31]:

# Constraints
constraints = ({'type':'eq','fun': lambda weight: np.sum(weight)-1},
               {'type':'eq','fun': lambda weight: calculate_returns(weight) - possible_return})

# Constraints constraints = ({'type':'eq','fun': lambda weight: np.sum(weight)-1}, {'type':'eq','fun': lambda weight: calculate_returns(weight) - possible_return})

In [32]:

# Now loop for different expected returns:
frontier_volatility = []
weights_opt = pd.DataFrame(columns=range(n))
for possible_return in expected_returns_range:
    # function for return
    result = minimize(calculate_volatility,equal_weights,bounds=bounds,constraints=constraints)
    frontier_volatility.append(result['fun'])
    weights_opt = pd.concat([weights_opt, pd.DataFrame(result['x']).T])

# Now loop for different expected returns: frontier_volatility = [] weights_opt = pd.DataFrame(columns=range(n)) for possible_return in expected_returns_range: # function for return result = minimize(calculate_volatility,equal_weights,bounds=bounds,constraints=constraints) frontier_volatility.append(result['fun']) weights_opt = pd.concat([weights_opt, pd.DataFrame(result['x']).T])

Plot Efficient Frontier¶

In [33]:

plt.figure(figsize=(12,8))
plt.scatter(mc_portfolio_vol,mc_portfolio_returns,c=mc_sharpe_ratios)
plt.ylabel('Expected Returns')
plt.xlabel('Expected Volatility')
plt.colorbar(label='Sharpe Ratio')
# Add frontier line
plt.plot(frontier_volatility,expected_returns_range,'r-',linewidth=4);

plt.figure(figsize=(12,8)) plt.scatter(mc_portfolio_vol,mc_portfolio_returns,c=mc_sharpe_ratios) plt.ylabel('Expected Returns') plt.xlabel('Expected Volatility') plt.colorbar(label='Sharpe Ratio') # Add frontier line plt.plot(frontier_volatility,expected_returns_range,'r-',linewidth=4);