Traveling Salesperson Problem¶

The Traveling Salesperson Problem (TSP) is a classic optimization problem in computer science and operations research. It involves finding the most efficient route for a salesperson to visit a set of cities and return to the starting city, with the goal of minimizing travel distance or cost.

Problem Definition¶

Given:

• A list of cities (or nodes).
• The distances or costs between each pair of cities.

Objective:

• Find the shortest possible route that visits each city exactly once and returns to the starting city.

Example¶

• Suppose there are four cities: A, B, C, and D.
• The distances between them are:

A	B	C	D	E
A → B: 10
A → C: 15	B → C: 35
A → D: 20	B → D: 25	C → D: 30
A → E: 12	B → E: 17	C → E: 26	D → E: 23
A → F: 24	B → F: 28	C → F: 13	D → F: 13	E → F: 27

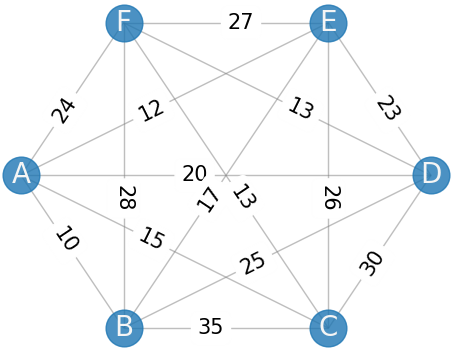
The task is to determine the sequence of cities (e.g., A → B → C → D → E → F → A) that minimizes the total distance traveled.

Applications¶

1. Logistics and Delivery: Optimizing routes for delivery trucks or couriers.
2. Manufacturing: Designing efficient robotic arms or conveyor belts.
3. Tourism: Creating optimal travel itineraries.

Complexity¶

• Computationally Hard: TSP is NP-hard, meaning there's no known polynomial-time algorithm to solve it for all cases.
• For (n) cities, there are ((n-1)!) possible routes.

Solution Approaches¶

1. Exact Algorithms:

   • Brute Force: Explore all possible routes (impractical for large (n)).
   • Dynamic Programming.
   • Mixed Integer Linear Programming (MILP).

2. Heuristic and Approximation Methods:

   • Greedy Algorithms.
   • Genetic Algorithms.
   • Simulated Annealing.
   • Ant Colony Optimization.

3. Machine Learning

Mixed-Integer Linear Program (MILP) Formulation¶

The Traveling Salesperson Problem (TSP) can be formulated as a Mixed-Integer Linear Program (MILP). Below is a typical formulation:

Sets¶

• $i$, $j$: Cities (nodes).

Parameters¶

• $ c_{ij} $: Cost or distance of traveling from city $i$ to city $j$.
• $ n $: Number of cities.

Variables¶

1. Decision Variables:

   • $ x_{ij} \in \{0, 1\} $: Binary variable indicating whether the path from city $i$ to city $j$ is included in the tour.
     • $ x_{ij} = 1 $: Path from city $i$ to $j$ is used.
     • $ x_{ij} = 0 $: Path from city $i$ to $j$ is not used.

2. Auxiliary Variables (for subtour elimination):

   • $ u_i $: A continuous variable representing the order in which city $i$ is visited, used to eliminate subtours.

Objective Function:¶

Minimize the total travel cost: $$ \min_{x_{ij}, u_i} \quad \sum_{i=1}^{n} \sum_{j=1, j \neq i}^{n} c_{ij} x_{ij} $$

Constraints:¶

1. Each city is entered exactly once: $$ \sum_{i=1, i \neq j}^{n} x_{ij} = 1 \quad \forall j = 1, \dots, n $$

2. Each city is exited exactly once: $$ \sum_{j=1, j \neq i}^{n} x_{ij} = 1 \quad \forall i = 1, \dots, n $$

3. Subtour elimination constraints (Miller-Tucker-Zemlin formulation): $$ u_i - u_j + n \cdot x_{ij} \leq n - 1 \quad \forall i, j = 2, \dots, n, \; i \neq j $$ $$ 1 \leq u_i \leq n - 1 \quad \forall i = 2, \dots, n $$

   The basic formulation with decision variables $x_{ij}$ ensures each city is visited exactly once but does not inherently prevent subtours (i.e., tours that visit only a subset of cities). These constraints force the auxiliary variable $u_i$ to ensure that a valid sequence of cities is followed. If $x_{ij} = 1$ (i.e., there is a path from $i$ to $j$), then $u_i < u_j$.

Pyomo formulation¶

In [1]:

# Import libraries
import numpy as np
import pandas as pd
import pyomo.environ as pyo
from pyomo.core.util import quicksum
import highspy

# Import libraries import numpy as np import pandas as pd import pyomo.environ as pyo from pyomo.core.util import quicksum import highspy

In [2]:

# Pyomo model
def pyomo_model(n: int):
    """
    
    :param n: Number of cities
    :return: algrebaic model
    """
    
    tsp = pyo.AbstractModel()
    
    # Sets
    tsp.i = pyo.RangeSet(1, n)
    tsp.j = pyo.RangeSet(1, n)
    
    # Parameters
    tsp.C_ij = pyo.Param(tsp.i, tsp.j, doc='Cost of traveling from i to j')
    
    # Variables
    tsp.x_ij = pyo.Var(tsp.i, tsp.j, doc='Indicates whether the path from i to j is included', within=pyo.Binary)
    tsp.u_i = pyo.Var(tsp.i, doc='Represents the order in which i is visited', bounds=(1, n-1), within=pyo.PositiveReals)
    
    # Model definition
    # Objective Function
    tsp.objective = pyo.Objective(rule=objective, sense=pyo.minimize, doc='Minimize Cost')
    # Add Constraints
    tsp.c_visit_once = pyo.Constraint(tsp.j, rule=c_visit_once, doc='Visit Once')
    tsp.c_leave_once = pyo.Constraint(tsp.i, rule=c_leave_once, doc='Leave Once')
    tsp.c_subtour_elimination = pyo.Constraint(tsp.i, tsp.j, rule=c_subtour_elimination, doc='Subtour Elimination')
    
    return tsp
    
# Objective function
def objective(m):
    return quicksum(m.C_ij[i, j] * m.x_ij[i, j] for i in m.i for j in m.j if j!=i)

# Constraints
def c_visit_once(m, j):
    return sum(m.x_ij[i, j] for i in m.i if j!=i) == 1

def c_leave_once(m, i):
    return sum(m.x_ij[i, j] for j in m.j if j!=i) == 1

def c_subtour_elimination(m, i, j):
    if i != j and i>=2 and j>=2:
        return m.u_i[i] - m.u_i[j] + len(m.i) * m.x_ij[i, j] <= len(m.i) - 1
    return pyo.Constraint.Skip

# Pyomo model def pyomo_model(n: int): """ :param n: Number of cities :return: algrebaic model """ tsp = pyo.AbstractModel() # Sets tsp.i = pyo.RangeSet(1, n) tsp.j = pyo.RangeSet(1, n) # Parameters tsp.C_ij = pyo.Param(tsp.i, tsp.j, doc='Cost of traveling from i to j') # Variables tsp.x_ij = pyo.Var(tsp.i, tsp.j, doc='Indicates whether the path from i to j is included', within=pyo.Binary) tsp.u_i = pyo.Var(tsp.i, doc='Represents the order in which i is visited', bounds=(1, n-1), within=pyo.PositiveReals) # Model definition # Objective Function tsp.objective = pyo.Objective(rule=objective, sense=pyo.minimize, doc='Minimize Cost') # Add Constraints tsp.c_visit_once = pyo.Constraint(tsp.j, rule=c_visit_once, doc='Visit Once') tsp.c_leave_once = pyo.Constraint(tsp.i, rule=c_leave_once, doc='Leave Once') tsp.c_subtour_elimination = pyo.Constraint(tsp.i, tsp.j, rule=c_subtour_elimination, doc='Subtour Elimination') return tsp # Objective function def objective(m): return quicksum(m.C_ij[i, j] * m.x_ij[i, j] for i in m.i for j in m.j if j!=i) # Constraints def c_visit_once(m, j): return sum(m.x_ij[i, j] for i in m.i if j!=i) == 1 def c_leave_once(m, i): return sum(m.x_ij[i, j] for j in m.j if j!=i) == 1 def c_subtour_elimination(m, i, j): if i != j and i>=2 and j>=2: return m.u_i[i] - m.u_i[j] + len(m.i) * m.x_ij[i, j] <= len(m.i) - 1 return pyo.Constraint.Skip

In [3]:

cost = [[ 0, 10, 15, 20, 12, 24],
        [10,  0, 35, 25, 17, 28],
        [15, 35,  0, 30, 26, 13],
        [20, 25, 30,  0, 23, 13],
        [12, 17, 26, 23,  0, 27],
        [24, 28, 13, 13, 27,  0]]
n = len(cost)
c_ij = {(i+1, j+1): cost[i][j] for i in range(n) for j in range(n)}

cost = [[ 0, 10, 15, 20, 12, 24], [10, 0, 35, 25, 17, 28], [15, 35, 0, 30, 26, 13], [20, 25, 30, 0, 23, 13], [12, 17, 26, 23, 0, 27], [24, 28, 13, 13, 27, 0]] n = len(cost) c_ij = {(i+1, j+1): cost[i][j] for i in range(n) for j in range(n)}

In [4]:

# Data
data = {
    None: {
        # Parameters
        'C_ij': c_ij
    }
}

# Data data = { None: { # Parameters 'C_ij': c_ij } }

In [5]:

# Create instance model
tsp = pyomo_model(n)
tsp_instance = tsp.create_instance(data)

# Create instance model tsp = pyomo_model(n) tsp_instance = tsp.create_instance(data)

In [6]:

# Solve problem with Highspy
solver = pyo.SolverFactory('appsi_highs')
solver.solve(tsp_instance, tee=True)

# Solve problem with Highspy solver = pyo.SolverFactory('appsi_highs') solver.solve(tsp_instance, tee=True)

Coefficient ranges:
  Matrix [1e+00, 6e+00]
  Cost   [1e+01, 4e+01]
  Bound  [1e+00, 5e+00]
  RHS    [1e+00, 5e+00]
Presolving model
32 rows, 35 cols, 120 nonzeros  0s
32 rows, 35 cols, 120 nonzeros  0s
Objective function is integral with scale 1

Solving MIP model with:
   32 rows
   35 cols (30 binary, 0 integer, 0 implied int., 5 continuous)
   120 nonzeros

        Nodes      |    B&B Tree     |            Objective Bounds              |  Dynamic Constraints |       Work      
     Proc. InQueue |  Leaves   Expl. | BestBound       BestSol              Gap |   Cuts   InLp Confl. | LpIters     Time

         0       0         0   0.00%   0               inf                  inf        0      0      0         0     0.0s
         0       0         0   0.00%   90.4            inf                  inf        0      0      0        17     0.0s
 R       0       0         0   0.00%   90.4            91                 0.66%       26      4      0        23     0.0s

Solving report
  Status            Optimal
  Primal bound      91
  Dual bound        91
  Gap               0% (tolerance: 0.01%)
  Solution status   feasible
                    91 (objective)
                    0 (bound viol.)
                    0 (int. viol.)
                    0 (row viol.)
  Timing            0.00 (total)
                    0.00 (presolve)
                    0.00 (postsolve)
  Nodes             1
  LP iterations     23 (total)
                    0 (strong br.)
                    6 (separation)
                    0 (heuristics)

Out[6]:

{'Problem': [{'Lower bound': 91.0, 'Upper bound': 91.0, 'Number of objectives': 1, 'Number of constraints': 0, 'Number of variables': 0, 'Sense': 1}], 'Solver': [{'Status': 'ok', 'Termination condition': 'optimal', 'Termination message': 'TerminationCondition.optimal'}], 'Solution': [OrderedDict({'number of solutions': 0, 'number of solutions displayed': 0})]}

In [7]:

# Display results
x_ij = tsp_instance.x_ij.extract_values()
C_ij = tsp_instance.C_ij.extract_values()
u_i = tsp_instance.u_i.extract_values()
u_i[1] = 0  # First city
u_i = [k for k, v in sorted(u_i.items(), key=lambda item: item[1])]
u_i.append(1)  # Come back to first city
for i in range(len(u_i)-1):
    print(f"Travel from {u_i[i]} to {u_i[i+1]} and Cost {C_ij[(u_i[i],u_i[i+1])]}")

# Display results x_ij = tsp_instance.x_ij.extract_values() C_ij = tsp_instance.C_ij.extract_values() u_i = tsp_instance.u_i.extract_values() u_i[1] = 0 # First city u_i = [k for k, v in sorted(u_i.items(), key=lambda item: item[1])] u_i.append(1) # Come back to first city for i in range(len(u_i)-1): print(f"Travel from {u_i[i]} to {u_i[i+1]} and Cost {C_ij[(u_i[i],u_i[i+1])]}")

Travel from 1 to 3 and Cost 15
Travel from 3 to 6 and Cost 13
Travel from 6 to 4 and Cost 13
Travel from 4 to 5 and Cost 23
Travel from 5 to 2 and Cost 17
Travel from 2 to 1 and Cost 10